TorchMetrics — PyTorch Metrics Built to Scale

Machine learning metrics making evaluations of distributed PyTorch models clean and simple.

Figuring out which metrics you need to evaluate is key to deep learning. There are various metrics that we can evaluate the performance of ML algorithms. TorchMetrics is a collection of PyTorch metric implementations, originally a part of the PyTorch Lightning framework for high-performance deep learning. This article will go over how you can use TorchMetrics to evaluate your deep learning models and even create your own metric with a simple to use API.

What is TorchMetrics?

TorchMetrics is an open-source PyTorch native collection of functional and module-wise metrics for simple performance evaluations. You can use out-of-the-box implementations for common metrics such as Accuracy, Recall, Precision, AUROC, RMSE, R² etc. or create your own metric. We currently support over 25+ metrics and are continuously adding more general tasks and domain-specific metrics (object detection, NLP, etc.).

Initially created as a part of Pytorch Lightning (PL), TorchMetrics is designed to be distributed-hardware compatible and work with DistributedDataParalel(DDP) by default. All metrics are rigorously tested on CPUs and GPUs.

Using TorchMetrics

Installation

This package can be installed from PyPI with:

pip install torchmetrics

Or directly from source-code from GitHub repository:

# with source
pip install https://github.com/PyTorchLightning/metrics/archive/refs/heads/master.zip

Functional Metrics

Similar to torch.nn, most metrics have both a module-based and a functional version. The functional versions implement the basic operations required for computing each metric. They are simple python functions that, as input, take torch.tensors and return the corresponding metric as a torch.tensor. The code snippet below shows a simple example for calculating the accuracy using the functional interface:

Module Metrics

Nearly all functional metrics have a corresponding module-based metric that calls it a functional counterpart underneath. The module-based metrics are characterized by having one or more internal metrics states (similar to the parameters of the PyTorch module) that allow them to offer additional functionalities:

• Accumulation of multiple batches
• Automatic synchronization between multiple devices
• Metric arithmetic

The code below shows how to use the module-based interface:

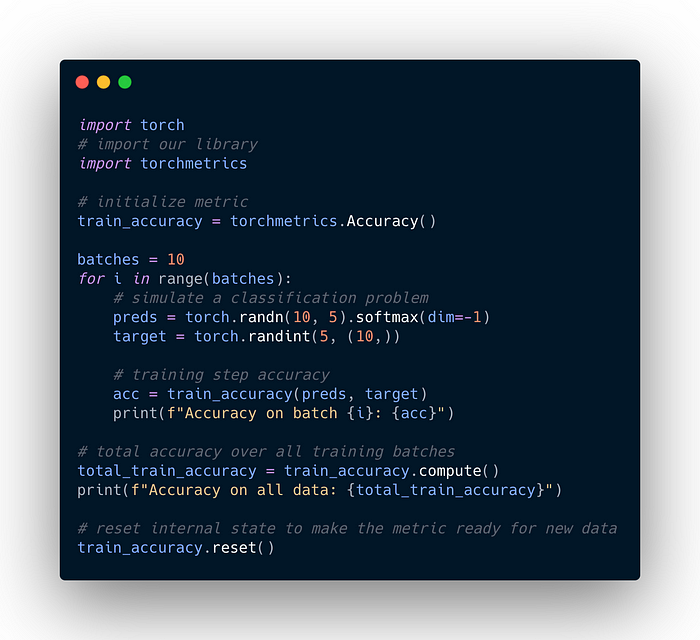
Each time we call the forward function of the metric, we simultaneously calculate the metric on the current batch of data we are seeing and update the internal metric state that keeps track of all data seen until now. The internal state needs to be reset between epochs and should not be mixed across training, validation, and testing. We therefore highly recommend to re-initialize the metric per mode as shown below:

TorchMetrics in Lightning

The example below shows how to use a metric in your LightningModule:

While TorchMetrics was built to be used with native PyTorch, using TorchMetrics with Lightning offers additional benefits:

• Module metrics are automatically placed on the correct device when properly defined inside a LightningModule. This means that your data will always be placed on the same device as your metrics.
• Native support for logging metrics in Lightning using self.log inside your LightningModule. Lightning will log the metric based on on_step and on_epoch flags present in self.log(…). If on_epoch=True, the logger automatically logs the end of epoch metric value by calling .compute().
• The .reset() method of the metric will automatically be called and the end of an epoch.

Converting from Lightning

Users already familiar with the metrics interface from Lightning should have no problem getting used to TorchMetrics. Replace:

from pytorchlightning import metrics

with:

import torchmetrics

and you should be good to go.

Note that metrics will be part of PyTorchLightning until v1.3 but will no longer receive any updates. We highly recommend that users switch to TorchMetrics to get any bug fixes and enhancements we may implement.

Implementing Your Own Metric

If you are looking to use a metric that is not yet supported, you can use TorchMetrics’ API to implement your own custom metric by simply subclassing torchmetrics.Metric and implementing the following methods:

1. __init__(): Each state variable should be called using self.add_state(…).
2. update(): Any code needed to update the internal metrics states for accumulation given any inputs to the metric.
3. compute(): Computes a final value from the state of the metric.

Example: Root mean squared error

Root mean squared error is a great example of why many metric computations need to be divided into two functions. It is defined as:

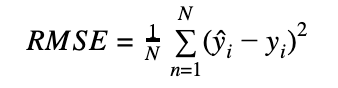
To properly calculate RMSE, we need two metric states: sum_squared_error to keep track of the squared error between the target y and the predictions y and n_observations to know how many observations we have encountered.

Because sqrt(a+b) != sqrt(a) + sqrt(b) we cannot implement this metric as a simple mean of the RMSE score calculated per batch and instead needs to implement all logic that needs to happen before the square root in an update step and the remaining in compute.

Choosing the Right Metric for Your Model

Choosing the correct metric is significant for determining if your model performs as it should or if something is wrong.

Predicting Coronavirus

Assume that you are tasked with building a classification network that can determine from a set of non-invasive measurements if a patient is Coronavirus positive. You are given a few thousands of observations, and using your favourite network architecture, you optimize to identify which patients have Coronavirus correctly. This model can make sure patients who have tested positive are isolated to avoid transmitting the virus and quickly get treatment.

To evaluate your model, you calculated 4 metrics: accuracy, confusion matrix, precision, and recall. You got the following results:

Accuracy score: 99.9%.

Confusion matrix:

Precision score: 1.0

Recall score: 0.28

Evaluating the Scores

What would you say? Is the model good enough? Let’s dive a little deeper to understand what these metrics mean.

In classification, accuracy means the fraction of predictions our model got right. Or, more formally,

Our model got an extremely high accuracy score: 99.9%. It seems that the network is doing exactly what you asked it to do, and you can accurately detect if a patient has the Coronavirus.

Another useful metric for binary classification is the confusion matrix. This gives us the following combination of true and false positives and negatives.

from understanding confusion matrix by Sarang Narkhede

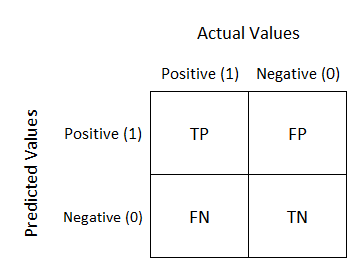
We can quickly determine two things from the confusion matrix:

* The number of negative patients far unweight the number of positive patients -> this means your dataset is highly unbalanced.

* You failed to detect 5 patients that have corona.

Looking at accuracy, the model seems to be performing very well. Still, taking the confusion matrix into account, we learn that the model was too focused on predicting negative patients and failed to predict the positive ones. In this setting, it should be clear that there is a huge difference between correctly identifying a patient with corona than correctly identifying one that does not: Correctly identifying a patient with corona will make sure the patient gets treatment early on and, most importantly gets isolated, so they don’t infect others.

Why did the accuracy metric not show that something was wrong with the model? Accuracy captures the overall performance to predict all classes, wherein this case correctly, and we are interested in a metric that captures how well we are predicting the true positives. Therefore, you turn your attention to Precision and Recall.

Precision is defined as the proportion of positive identifications that are actually correct. Or, more formally,

where TP and FP represent the number of true positives and false positives, respectively, a model with 0 false positives will have a precision score of 1.0, and a model where all the positive results were actually false will have a precision score of 0.

Recall is defined as the proportion of actual positives was identified correctly.

Or formally:

Where TP and FN represent the number of true positives and false negatives, respectively. Similarly, a model will have a recall score of 1.0 if it has no false negatives.

From the definitions, we can conclude that precision focuses on the “cost” of not identifying all false positives, whereas recall focuses on the “cost” of not identifying all false negatives. Because it is the false-negative we are interested in here, we should re-evaluate our model under the recall metric now getting a score of 0.28. You have now quantified that your model is not performing well, and you probably need to deal with the huge class imbalance that exists in the dataset while training your machine learning algorithm.

This small example showcases the importance of choosing the correct metric for evaluating your machine learning algorithms. In general, it is recommended to evaluate algorithms using a collection of metrics because all of them focus on different aspects of data and model predictions.

Contribute!

We want to thank all the contributors who made this library possible! The Lightning + TorchMetrics team is hard at work adding even more metrics, but to grow more quickly, we need your help.

Join our Slack community to learn more about contributing to open source.